圣诞树
You cannot submit for this problem because the contest is ended. You can click "Open in Problem Set" to view this problem in normal mode.
Description
简化题意
给定一棵树,现在你要选择一个点集 ,使得 ,而且 ,求 的最大值。
其中, 表示第 个节点的深度。规定这棵树根节点为 ,其深度为 。
小北在圣诞节获得了一颗圣诞树,神奇的是这颗圣诞树上有 片叶子和 条连接叶子的边,也就是说这真的是一颗“树”。特别的,这棵圣诞树的根为 ,根的深度为 。
现在小北共有 个彩灯,小北将要把彩灯放在圣诞树上。小北觉得,彩灯越往上放越好看,也就是说节点的深度越浅越好看,因此如果彩灯被挂在第 片叶子上,其美丽值为 。
小北不会把所有彩灯都挂上。具体地,若小北挂上的彩灯组成的集合为 ,则 应该是集合内的彩灯的最上面一个(深度最小)且是集合内的彩灯的最美丽的一个 , 是第二靠上的且是第二美丽的,依次类推。注意小北允许有彩灯被挂在同一层上。
问整棵树的彩灯美丽值之和最大是多少。
Input
本题共读入 行。
- 第 行: 个整数 ,表示树的节点数;
- 第 行:第 行 个整数 ,表示第 条边连接 和 。
Output
- 输出仅 行 个整数:整棵树的最大的彩灯美丽值之和。
Sample
5
1 2
5 2
2 3
4 1
13
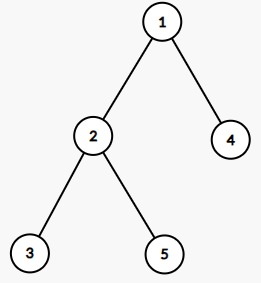
选择 这些节点,满足 ,且 。其中 表示第 个节点的美丽值, 表示第 个节点的深度。其总美丽值为 。
5
1 2
1 3
2 4
2 5
15
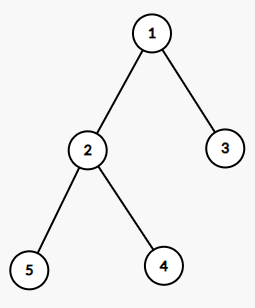
选择所有点即可。
Limitation
| 特殊性质 | 得分 | ||
|---|---|---|---|
| 无 | |||
| 或 | |||
| 无 | |||
- 对于 的数据,,保证输入数据可以构成一颗树。
[北辰杯 North-Star-Cup] 九月月赛
- Status
- Done
- Rule
- Ledo
- Problem
- 6
- Start at
- 2023-9-22 18:00
- End at
- 2023-9-23 0:00
- Duration
- 6 hour(s)
- Host
- Partic.
- 75

