You cannot submit for this problem because the contest is ended. You can click "Open in Problem Set" to view this problem in normal mode.

题目背景

纵横交错二，盘根错节

题目描述

辰辰对多叉堆有自己独特的见解，多叉堆是一种树形数据结构，本题中我们只考虑小根堆，它满足除了根以外的结点，每个点的权值都不小于父亲的权值。除了叶结点，每个点有至少一个子结点。

初始时有 $n$ 个结点，编号分别为 $0 \sim n - 1$ ，每个结点都是一棵以自身为根的单点树。接下来按顺序有 $q$ 次操作，每次操作有以下两种：

• 1 x y：选择不在同一棵树里的结点 $x$ 和 $y$，将 $x$ 所在树的根直接接在 $y$ 所在树的根之下，此时 $x$ 和 $y$ 所在树将合并为同一棵树。
• 2 x：选择结点 $x$，设 $x$ 当前所在树的结点数为 $size$。你需要计算将 $0 \sim size - 1$ 这 $size$ 个数分别填入 $x$ 所在树的结点中，能够产生多少种不同的多叉堆。两种堆不同当且仅当存在某个结点填入的值不同。由于答案可能很大，你只需要求出答案模 $10^9+7$ 后的结果。

输入格式

第一行两个整数 $n, q$，具体含义见题目描述。

接下来 $q$ 行每行可能是下面两种格式之一：

• 1 x' y'：你需要通过计算 $x=(x'+ans) \bmod n , y=(y'+ans) \bmod n$ 来得到真正的 $x$ 和 $y$，输入保证 $x$ 和 $y$ 所在树不同。
• 2 x'：你需要通过计算 $x=(x'+ans) \bmod n$ 来得到真正的 $x$。

其中 $ans$ 表示上一次 $2$ 操作的输出结果 ，初始时 $ans=0$。

输出格式

对于每次 $2$ 操作输出一行一个整数表示答案。

5 6
1 1 0
1 2 0
2 1
1 3 1
1 2 0
2 4

2
8

提示

【输入输出样例 1 说明】

第 $1$ 次操作时，将 $1$ 所在树的根 $1$ 接在 $0$ 所在树的根 $0$ 下。

第 $2$ 次操作时，将 $2$ 所在树的根 $2$ 接在 $0$ 所在树的根 $0$ 下。

第 $3$ 次操作时，$1$ 所在树如图 $1$，在 $0,1,2$ 中分别填入 $[0,1,2]$ 和 $[0,2,1]$ 可以产生 $2$ 种不同的堆。

第 $4$ 次操作时 $x=(3+2) \bmod 5=0$，$y=(1+2) \bmod 5=3$，将 $0$ 所在树的根 $0$ 接在 $3$ 所在树的根 $3$ 下。

第 $5$ 次操作 时，$x=(2+2) \bmod 5=4$，$y=(0+2) \bmod 5=2$，将 $4$ 所在树的根 $4$ 接在 $2$ 所在树的根 $3$ 下。

第 $6$ 次操作 时，$x=(4+2) \bmod 5=1$，$1$ 所在树如图 $2$，在 $0\sim 4$ 中分别填入 $[1,2,3,0,4]$，$[1,3,2,0,4]$，$[1,2,4,0,3]$，$[1,4,2,0,3]$，$[1,3,4,0,2]$，$[1,4,3,0,2]$，$[2,4,3,0,1]$ 可以产生 $8$ 种不同的堆。

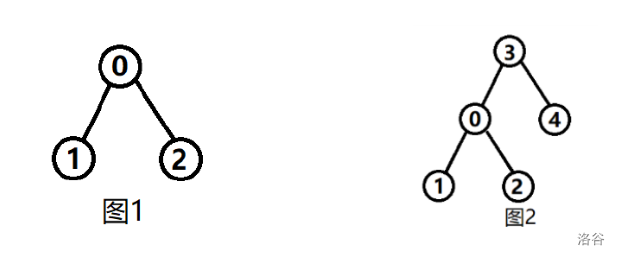
【数据规模与约定】

对于 $100\%$ 的数据，$0\le x',y' <n \le 3\times 10^5$，$1\le Q\le 3\times 10^5$。

对于不同测试点，我们约定

特殊性质 $1$：存在 $1\le i<n$，前 $i$ 次操作均为 $1$ 操作，之后全是 $2$ 操作。

特殊性质 $2$：对于所有输入 $x$ 和 $y$ 本身即是其所在树的根。