#F. CSP-J 初赛模拟卷A

Type: Objective

You cannot submit for this problem because the contest is ended. You can click "Open in Problem Set" to view this problem in normal mode.

一、单项选择题（共15题，每题2分，共计30分；每题有且仅有一个正确选项)

在标准 $\text{ASCII}$ 码表中，已知英文字母 $Z$ 的 $\text{ASCII}$ 码十进制表示是 $90$ ，那么英文字母 $B$ 的 $\text{ASCII}$ 码二进制表示是（ )。 {{ select(1) }}

01000001
01000010
01000011
01000000

2.以下关于 $CSP$ 与 $NOIP$ 的描述正确的是（ ) {{ select(2) }}

A.CSP属于非专业认证，只有在校生才能参加
B.CSP是中国电子学会举办的程序设计竞赛
C.CSP和NOIP毫无关系，没参加CSP也可以直接参加 NOIP
D.CSP和NOIP都是CCF旗下的程序设计赛事

3.以下不能用作 $C++$ 程序中的标识符的是（ )。 {{ select(3) }}

A.private
B.friends
C.news
D.pascal

NOI复赛测评机所用的 Linux系统属于( )。 {{ select(4) }}

A. $UML$
B. $IDE$
C. $OS$
D. $Database$

如果65536种颜色用二进制编码来表示，至少需要( ）个二进制位。 {{ select(5) }}

A.16
B.8
C.12
D.10

6.搜索算法中的BFS算法经常用到的数据结构是（ )。 {{ select(6) }}

A.堆
B.栈
C.链表
D.队列

7.在已经从小到大排好序的 $n$ 元素单向链表中查询是否存在关键字为 $k$ 的元素，最坏情况下运行的时间复杂度是（ ). {{ select(7) }}

A. $O(logn)$
B. $O(n)$
C. $O(n^2)$
D. $O(nlogn)$

8.在下列各种排序算法中，不是以“比较”作为主要操作的算法是（) {{ select(8) }}

A.归并排序
B.快速排序
C.冒泡排序
D.桶排序

9.关于计算机网络，下面的说法中正确的是（）。 {{ select(9) }}

A.现在的计算机必须连接到互联网才能正常运行
B.192.168.0.1是A类IP地址
C.互联网的诞生用到了现代计算机技术和现代通信技术
D.接入互联网的计算机的IP地址已经全部升级到了IPv6地址

将(2,6,10,17)分别存储到某个地址区间为0~10的哈希表中，如果哈希函数h(x)。( )，将不会产生冲突，其中ab表示a除以b的余数，sqrt表示开平方，floor表示向下取整。 {{ select(10) }}

A. $x\%11$
B. $x^2\%11$
C. $2x\%11$
D. $floor(sqrt(x))\%11$

11.现在有一个十六进制数27，它等于二进制数的（ )。 {{ select(11) }}

A.100011
B.100101
C.100111
D.100011

12.以下逻辑表达式中，不管A、B如何取值，恒为假的是（ )。 {{ select(12) }}

A. $(\neg A\vee B)\wedge (A\vee B)\wedge A$
B. $((\neg A\vee B)\vee (A\vee \neg B))\wedge B$
C. $A\wedge ((\neg A\vee B) \vee (A\vee \neg B))\wedge \neg A$
D. $((\neg A\vee B)\vee (A\vee \neg B))\wedge A\wedge \neg B$

13.某二叉树有16个结点都同时有左孩子结点和右孩子结点，则该二叉树中的叶子结点数是（）个。 {{ select(13) }}

A.19
B.17
C.18
D.16

14.现有16张不同的卡片，其中红、黄、蓝、绿色卡片各4张。从中任取3张，要求红色最多有1张并且3张卡片不能是同一种颜色，不同的取法组合共有（）种。 {{ select(14) }}

A.232
B.472
C.256
D.484

15.有8个结点的非连通无向图最多有( ）条边 {{ select(15) }}

A.8
B.7
C.21
D.49

二、阅读程序（程序输入不超过数组或字符串定义的范围，判断题正确填√，错误填×

除特殊说明外，判断题每题1.5分，选择题每题3分，共计40分）

(1)

#include <bits/stdc++.h>
using namespace std;
int gcd(int a, int b) {
    int tmp;
    if (b) tmp = a % b;	//第5行
    else return a;
    while (tmp) {
        a = b;
        b = tmp;
        tmp = a % b;
    }
    return b;
}

int lcm(int a, int b){
    return a / gcd(a, b) * b; //第15行
}
int main() {
    int a, b;
    cin >> a >> b;
    cout << gcd(a, b) << endl;
    return 0;
}

判断题

若输入0 2024，则输出结果为 0。 () {{ select(16) }}

true
false

将第5行中的 if(b) 改为if(0 != b) ，程序的运行结果不会改变。 () {{ select(17) }}

true
false

若输入2.4 4.8，则输出错误。 () {{ select(18) }}

true
false

将第15行 return a/gcd(a，b)*b 替换成 return a*b/gcd(a，b) ，程序的运行结果不会改变。() {{ select(19) }}

true
false

选择题

若输入数据为20244204 12348，则输出为（ )。. {{ select(20) }}

A.18
B.36
C.12
D.24

若将第20行cout << gcd(a，b)<< endl替换成cout<< lcm(a，b)<< endl，输入数据为20244204 12348，则输出为()。 {{ select(21) }}

A.6943761972
B. 程序出错，无输出
C.3471880986
D. 某个负数

(2)

#include <bits/stdc++.h>
using namespace std;
int main(){
	char s[128] = 10;
    cin.getline(s,128);
    for(int i = 0; i< strlen(s); ++i){
    	if(s[i]>= 65 && s[i] <= 90)[
        if(s[i]== 90){
        	s[i]= 65;
        }else{
        	s[i]+= 1;
        }
        s[i] ^=' ';
	}
    cout << s << endl;
    return 0;
}

判断题

输入一个长度大于128的字符串，程序的输出一定会出错。() {{ select(22) }}

true
false

将第6行cin.getline(s，128)更换为getline(cin，s)，程序的运行结果不变（) {{ select(23) }}

true
false

将第13行s[i]^=' '更换为s[i]^=32，程序的运行结果不变。 () {{ select(24) }}

true
false

将第9行if(s[i]==90)更换为if(slil=='z')。程序的运行结果不变() {{ select(25) }}

true
false

选择题

若输入字符串s为CSPjs2024，则输出为（）。 {{ select(26) }}

A.dtqjs2024
B.cspjs2024
C.DTQjs2024
D.CSPjs2024

27.若输出bcdea，则输入字符串s为( )。 {{ select(27) }}

A.BCDEA
B.ABCDZ
C.abcde
D.bcdez

(3)

#include <bits/stdc++.h>
using namespace std;
int used[20],a[20],n;
long long ret=0;
bool flag;
void dfs(int x)
{
	int i;
    if(x>n)
    {
    	flag=1;
        for(i=l;i<=n;i++)
        {
        	if(a[i]+i > n+2)
			{
				flag=0;
            	break;
			}
		}
		if(flag) ret++;
        return;
    }
	for(i=1 ;i<=n;i++)
	{
		if(used[i]==0)
		{
			used[i]=1, a[x]=i;
            dfs(x+1);
            used[i]=0, a[x]=0;	//26行
		}
	}
    
    
}
int main()
{
	cin>>n;
	dfs(1);
    cout<<ret;
    return 0;
}

判断题

如果输入n的值为0，那么程序在运行过程中一定会出现错误。 ( ) {{ select(28) }}

true
false

如果将第26行的a[x]=0去掉，输出的结果不会改变。 ( ) {{ select(29) }}

true
false

该程序算法的时间复杂度是 $O(n! \times n)$ 。 ( ) {{ select(30) }}

true
false

输入某个正整数n.程序运行的输出结果可能会等于0。（ ) {{ select(31) }}

true
false

选择题

若输入n=2，那么输出结果是（) {{ select(32) }}

A.1
B.2 。
C.3
D.0

若输入n=5，那么输出结果是（)。 {{ select(33) }}

A.16
B.5
C.10
D.12

34.（4分）若输出结果为128，则输入n是( )。 {{ select(34) }}

A.8
B.7
C.16
D.32

三、完善程序（单选题，每小题3分，共计30分）

（1）

输入一个十进制正整数 $n$ ，然后将 $n$ 转换为二进制数，最后统计二进制数的各位数字，看看一共有多少位为1，然后打印出总数。

输入格式：第1行输入十进制正整数 $n$ 。

输出格式：输出一个整数，表示十进制正整数n转换成的二进制数中有多少位为1。

输入样例：

输出样例：

样例说明：十进制数127转换为二进制数1111111，二进制位一共有7个1.所以输出7。

#include<bits/stdc++.h>
using namespace std;
int a[33],cnt;
int main()
{
	int n,sum,x;
    cin>>n;
    cnt=0;
    ①;
    while(x>0)
    {
    	a[②]=x%2;
        ③；
    }
    sum=0；
    for(int i=1;④;i++)
    {
    	if(a[i]==1)
			⑤;
    }
    cout<<sum<<endl;
    return 0;
}

①处应填() {{ select(35) }}

A.x=n
B.x=1
C.x=0
D.x=n-1

②处应填( )。 {{ select(36) }}

A.--cnt
B.++cnt
C.cnt--
D.cnt

③处应填（ )。 {{ select(37) }}

A.x/=2
B.n++
C.x++
D.n--

④处应填( )。 {{ select(38) }}

A.i<cnt
B.i<cnt/2
C.i<=cnt
D.i<=cnt/2

⑤处应填( )。 {{ select(39) }}

A.sum--
B.sum=x
C.sum=0
D.sum++

(2)

在一个 $n\times n$ 的棋盘上布满了0和1，如图（a)所示（n=7）。为叙述方便，将0用字母表示，如图(b)所示。

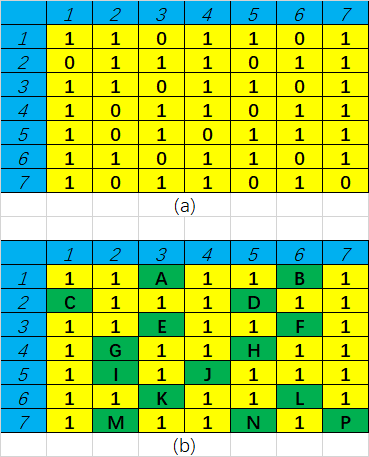
跳棋规则如下。

(i) 从某个 $0$ 格出发，可以向上、下、左、右 $4$ 个方向连续越过若干个(至少 $1$ 个） $1$ 格后跳入下一个 $0$ 格。如图(b)所示，从 $A$ 出发，可跳到 $B$ ，或者跳到 $E$ ，但不能直接跳到 $K$ 。在跳到 $B$ 之后还可以继续跳到 $F$ ，在跳到 $E$ 之后可继续跳到 $F$ 或 $K$ ，直到不能再跳为止。

(ii) 每个 $0$ 格只能到达一次，给出的起始点不能再次到达，也不能越过。跳过的鹿离为跳过 $1$ 格的个数加 $1$ ，如从 $A$ 到 $B$ ，跳过距离为 $3$ ，从 $B$ 到 $F$ ，跳过距离为 $2$ 。问题：当给出棋盘和起始点之后，最远能跳的距离是多少？如图（b）所示，从 $A$ 出发，可跳的路线不止一条，其中一条为： $A-B-F-L-K-E$ (可能不唯一）跳跃的距离为 3 2 3 3 3 它的跳过距离为 $14$ 。

输入格式：第 $1$ 行 $3$ 个整数 $n（1\len\le100）、x、y（xy$ 是起始点坐标，图（b）中 $A$ 处坐标为 $1，3)$ 。接下来 $n$ 行，每行 $n$ 个数 $(0$ 或 $1)$ ，数与数之间用一个空格分隔。输出格式：一个整数，即最大可跳距离（若不能跳，则输出 $0$ ）。

输入样例：

输出样例：

#include <bits/stdc++.h>
using namespace std;
int n,i,j,k,ans;
int a[105][105],vis[105][105]；//a 表示棋盘，vis统计点是否走过
int dx[4]={-1,1,0,0},dy[4]={0,0,1,-1};
void dfs(int x,int y,int step)
{
	ans = ①;
	for(int i=0;i<4;i++)
	{
		int tx=x,ty=y,s=0;
        while(tx+dx[i]>0 and tx+dx[i]<=n and ty+dy[i]>0 and ty+dy[i]<=n)
        {
        	tx+=dx[i];
	        ty+=dy[i];
	        S++；
	        if(②)
	        	break;
		}
		
        if(tx>0 and tx<=n and ty>0 and ty<=n and vis[tx][ty]==0 and a[tx][ty]==0 and s!=1)
		{
			vis[tx][ty]=1;
	        dfs(tx,ty,③);
	        ④; 
		}
	}


int main()
{
	int x,y,i,j;
	cin>>n>>x>>y;
	for(i=1;i<=n;i++)
	{
		for(j=1;j<=n;j++)
		{
			cin>>a[i][j];
		}
	}
	⑤;
	dfs(x,y,0);
	cout<<ans<<endl;
	return 0;
}

①处应填（) {{ select(40) }}

A.0
B.max(ans,step)
C.1
D.step

②处应填（ )。 {{ select(41) }}

A.vis[tx][ty]==1
B.vis[tx][ty] == 0
C.a[tx][ty]== 1
D.a[tx][ty]== 0

③处应填（ )。 {{ select(42) }}

A.step+s
B.step+1
C.step
D.step-1

④处应填( )。 {{ select(43) }}

A.vis[tx][ty]=1
B.vis[tx][ty]= 0
C.a[tx][ty]=1
D.a[tx][ty] = 0

⑤处应填( )。 {{ select(44) }}

A.a[x][y]=1
B.a[x][y]= 0
C.vis[x][y]=1
D.vis[x][y]= 0

初赛模拟卷A

Not Attended

Status: Done
Rule: OI
Problem: 6
Start at: 2024-8-13 16:15
End at: 2024-8-14 13:45
Duration: 2 hour(s)
Host: kunkka
Partic.: 36

#F. CSP-J 初赛模拟卷A

CSP-J 初赛模拟卷A

一、单项选择题（共15题，每题2分，共计30分；每题有且仅有一个正确选项)

二、阅读程序（程序输入不超过数组或字符串定义的范围，判断题正确填√，错误填×

除特殊说明外，判断题每题1.5分，选择题每题3分，共计40分）

(1)

判断题

选择题

(2)

判断题

选择题

(3)

判断题

选择题

三、完善程序（单选题，每小题3分，共计30分）

（1）

(2)

初赛模拟卷A

Status

Development

Support

#F. CSP-J 初赛模拟卷A

CSP-J 初赛模拟卷A

一、单项选择题（共15题，每题2分，共计30分；每题有且仅有一个正确选项)

二、阅读程序（程序输入不超过数组或字符串定义的范围，判断题正确填√，错误填×

除特殊说明外，判断题每题1.5分，选择题每题3分，共计40分）

(1)

判断题

选择题

(2)

判断题

选择题

(3)

判断题

选择题

三、完善程序（单选题，每小题3分，共计30分）

（1）

(2)

初赛模拟卷A

Status

Development

Support

Don't have an account?

SIGN IN