这寺豪德
You cannot submit for this problem because the contest is ended. You can click "Open in Problem Set" to view this problem in normal mode.
题目背景
豪德寺三花是一只招财猫。作为招财猫,她对有规则外形的三角形晶体很感兴趣。
她用招来的钱财买来了一个巨大的三角形迷宫样式的晶体。晶体由许多三角形晶格组成,由于特殊的性质,晶格之间有的可以互相到达,而有的不能。
于是三花想知道,从最顶上的晶格出发,可以到达多少个格子。这被认为是该晶体实际的价值。
题目描述
三花的晶体可被视为一个边长为 的三角形迷宫。迷宫最外围有一圈墙壁,内部则有部分位置为空,可以经过。

组成迷宫的每一个三角形可以视作组成迷宫的单元。为了便于描述迷宫内的墙壁,这里仅对绿色部分的三角形标号,第 行第 个绿色三角形被标号为 。描述这些三角形墙壁的情况就可以描述整个阵列的墙壁情况。具体方法详见输入格式。
现在询问,从三角形 出发,一共可以到达多少个小三角形?这些小三角形包含组成迷宫的所有单元,也即红色三角形与绿色三角形。
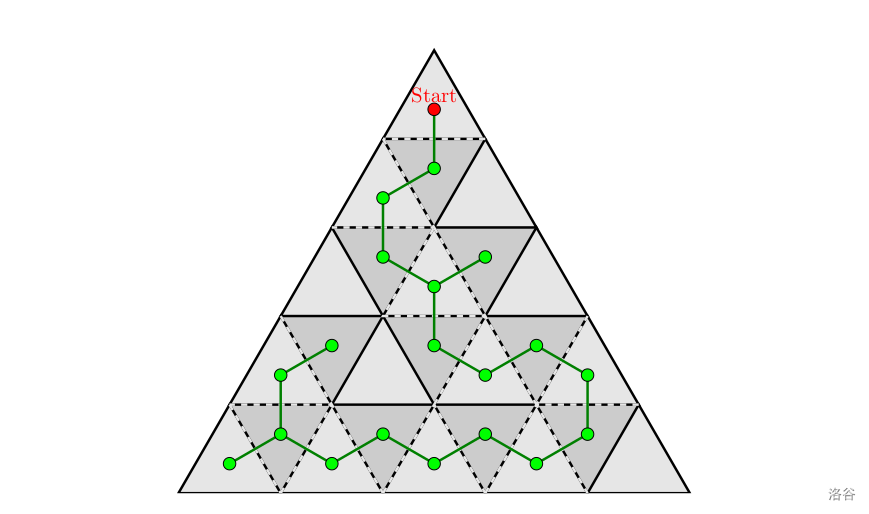
如图所示,途中所有灰色虚线表示可以通过的墙壁,红点表示出发位置所在三角形的中心,绿点表示从起点出发可以到达的三角形的中心。红点与绿点的数量之和为 ,也即可以到达 个不同的三角形单元。
输入格式
第一行有一个正整数 ,表示三角形阵列的边长。
接下来 行,第 行有 个整数,描述每个绿色三角形墙壁的情况。描述三角形 的整数 表示如下:
- 。
- 若三角形 右上侧可通过,则 ,否则 。
- 若三角形 正下方可通过,则 ,否则 。
- 若三角形 左上侧可通过,则 ,否则 。
可以发现, 的值可以唯一表示一个三角形三边墙壁的情况。
输入保证,整个三角形迷宫最外边一层的墙壁不可通过。
输出格式
输出共一行一个整数,表示从 出发可以到达的所有三角形(包括起点)的个数。
样例 #1
样例输入 #1
5
2
3 0
0 7 0
3 0 5 6
1 5 5 5 0
样例输出 #1
20
提示
数据范围及约定
特殊性质 :保证整个三角形迷宫只有最外面一层墙壁不可通过。 特殊性质 :可通过部分形成了一棵树。例如,样例可走部分即为一棵树。
对于全部数据,。
北辰OI算法提高班摸底测试
- Status
- Done
- Rule
- OI
- Problem
- 6
- Start at
- 2023-11-21 17:00
- End at
- 2023-11-30 1:00
- Duration
- 200 hour(s)
- Host
- Partic.
- 28

