醋溜便当
You cannot submit for this problem because the contest is ended. You can click "Open in Problem Set" to view this problem in normal mode.
题目背景
伊吹萃香是幻想乡的跟踪狂。
题目描述
萃香每天会派自己的分身巡视整个幻想乡。
幻想乡可以被视为一张 个点 条边的无向图,边有长度。萃香希望巡视到幻想乡的每个节点,于是她在每个节点 都安排了一个分身,分身会沿着一条路径从 出发再回到 。可以多次经过同一条边,也可以多次经过同一个点(包括 )。
如果分身巡视的路径太短,会被居民怀疑有跟踪的风险;如果路径太长,又增大了每个分身的工作量。于是萃香希望回路的长度在 之间。 均为整数,且 。
不过不是每个分身都能找到这样的回路。于是萃香会对于每个节点询问,是否存在一条从该节点出发的回路,长度在 之间。
输入格式
第一行有四个整数 ,含义如题面所示。
接下来 行,每行有三个整数 ,描述一条连接 的无向边,边权为 。
输出格式
输出共一行 个整数,之间用空格隔开。对于第 个整数,若点 可以找到一条长度在 之间的回路,则输出 ;否则输出 。
样例 #1
样例输入 #1
7 5 3 2
1 2 4
1 3 0
2 3 0
1 6 5
4 5 6
样例输出 #1
1 1 1 0 0 0 0
提示
样例解释
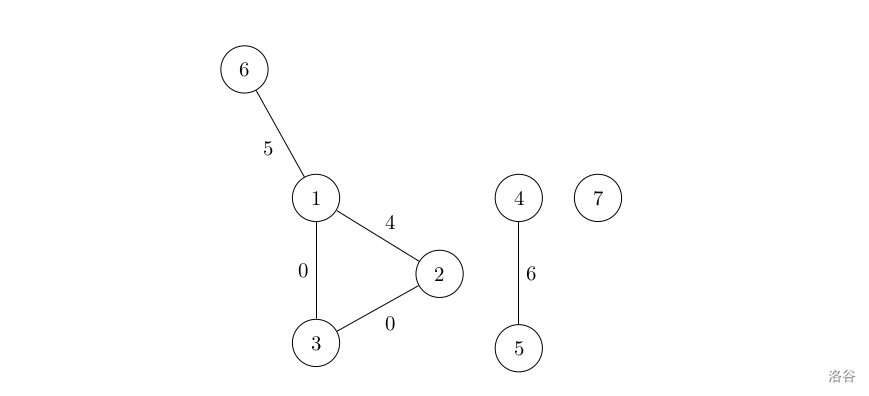
如图所示。对于前三个可以形成符合条件的回路的 个点,可能的情况如下:
- ,长度为 ,在 范围内;
- ,长度为 ,在 范围内;
- ,长度为 ,在 范围内;
对于剩下来的四个点:
- 只能形成 ,长度为 ,无法形成 内的回路;
- 与 的情况相同;
- 与 的情况相同;
- 无法形成回路。
数据范围及约定
特殊性质 :保证边权均为正数。
对于全部数据,,,,,并且有 。
北辰OI算法提高班摸底测试
- Status
- Done
- Rule
- OI
- Problem
- 6
- Start at
- 2023-11-21 17:00
- End at
- 2023-11-30 1:00
- Duration
- 200 hour(s)
- Host
- Partic.
- 28

